Il modo migliore per parlare di apprendimento supervisionato è quello individuare un caso semplice, ovvero l’apprendimento di una classe dai suoi esempi positivi e negativi, e successivamente generalizzare per di più classi. Come ultimo step per trattare l’apprendimento supervisionato bisogna parlare di regressione, dove gli output sono continui.
Diciamo che vogliamo imparare la classe C che identifica tutte le “auto familiari“. Abbiamo una serie di esempi di auto e abbiamo un gruppo di persone a cui mostriamo queste auto. Le persone guardano le auto per etichettarle; per esempi positivi intendiamo le auto che credono siano auto di famiglia mentre per esempi negativi le altre auto che credono non siano auto familiari.
L’apprendimento della classe consiste nel trovare una descrizione che sia condivisa da tutti gli esempi positivi e da nessuno degli esempi negativi.
Così facendo, possiamo fare una previsione: data un’auto che non abbiamo visto prima, verificando con la descrizione appresa, potremo dire se si tratta di un’auto di famiglia oppure no. Oppure possiamo estrarre della conoscenza e l’obiettivo potrebbe essere quello di capire cosa le persone si aspettano da un’auto di famiglia.
Dopo alcune discussioni con esperti del settore, diciamo che si arriva alla conclusione che tra tutte le caratteristiche che può avere un’auto, le caratteristiche che separano un’auto di famiglia dalle altre auto sono il prezzo e la potenza del motore.
Questi due attributi sono gli input per il riconoscitore di classe.
Nota: Stiamo considerando gli altri attributi come irrilevanti.
Sebbene si possa pensare ad altri attributi come il numero di posti a sedere e il colore che potrebbero essere importanti per distinguere tra i tipi di auto, prenderemo in considerazione solo il prezzo e la potenza del motore per mantenere questo esempio semplice.
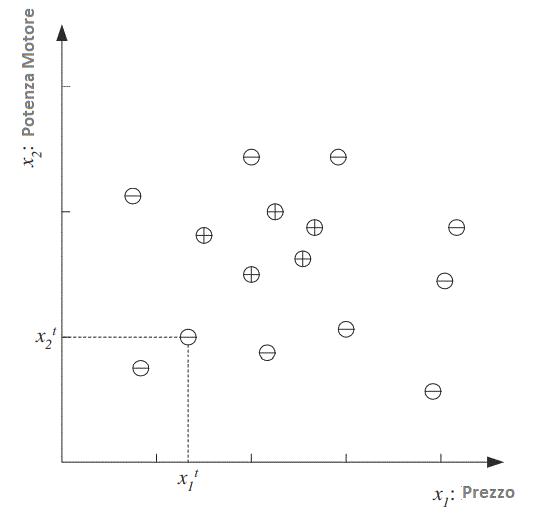
Ogni punto identificato dalla coppia (prezzo, motore) corrisponde ad un’auto di esempio. Il simbolo “+” denota un esempio positivo della classe mentre con “-” identifichiamo un esempio negativo ovvero un’auto non appartenente alla classe delle auto di famiglia.
Indichiamo il prezzo come primo attributo di input e la potenza del motore come secondo attributo (ad es. volume del motore in centimetri cubi), quindi rappresentiamo ciascuna auto utilizzando due valori numerici.
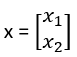
la sua etichetta ne denota il tipo.
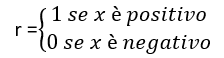
Ogni auto è rappresentata da una tale coppia ordinata (x,r) e il training set contiene N di questi esempi
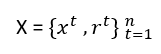
dove t rappresenta diversi esempi nell’insieme; non rappresenta il tempo o un ordine del genere
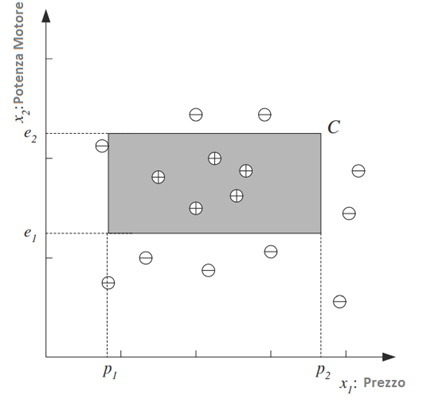
I nostri dati di allenamento possono ora essere tracciati nello spazio-bidimensionale :
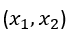
dove ogni istanza t è un punto dati di coordinate
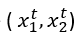
e il suo tipo, cioè positivo o negativo, è dato da
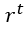
Dopo ulteriori analisi dei dati, potremmo avere motivo di ritenere che, affinché un’auto sia un’auto di famiglia, il suo prezzo e la potenza del motore dovrebbero rientrare in un determinato intervallo:
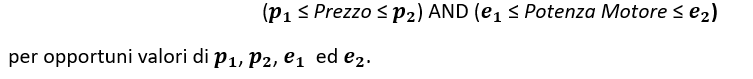
L’equazione assume quindi che C sia un rettangolo nello spazio bidimensionale di (Potenza Motore , Prezzo)
Inoltre, l’equazione, fissa l’ipotesi con cui descrivere C, cioè come l’insieme dei rettangoli.
L’ipotesi di classe, quindi, è corretta se per un input x, se e solo se h(x) = 1 per x positivo.
Supponiamo di avere un insieme di dati di addestramento X che è un sottoinsieme di tutti i possibili input, l’errore dell’ipotesi h dato il set di addestramento X è:

L’ ipotesi di classe H è l’insieme dei possibili rettangoli. Ogni quadrupla
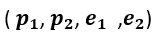
definisce un‘ ipotesi H e quello che a noi serve è capire quali sono i valori migliori della quadrupla . In altre parole, dobbiamo trovare i valori di questi 4 parametri partendo dall’insieme di dati di addestramento tale che:
il rettangolo risultante possa includere solo esempi positivi ed escludere quelli negativi.
