Per Classificazione si intende un’attività che richiede l’uso di algoritmi di Machine Learning che apprendono come assegnare un’etichetta di classe agli esempi dal dominio del problema.
Facciamo un esempio pratico.
Un credito è una somma di denaro prestata da un istituto finanziario, ad esempio una banca, da restituire con gli interessi, generalmente a rate.
È importante che la banca sia in grado di prevedere in anticipo il rischio connesso ad un prestito, che è la probabilità che il cliente vada in default e non restituisca l’intero importo, sia per assicurarsi che la banca realizzi un profitto e anche per non infastidire un cliente con un prestito oltre la sua capacità finanziaria.
Nel credit scoring, la banca calcola il rischio dato l’importo del credito e le informazioni sul cliente. Le informazioni sul cliente includono dati a cui abbiamo accesso e sono rilevanti per il calcolo della sua capacità finanziaria, vale a dire, reddito, risparmi, garanzie reali, professione, età, storia finanziaria passata, ecc. La banca ha un registro dei prestiti passati contenente tali dati del cliente e se il prestito è stato rimborsato o meno. Da questi dati, lo scopo è quello di inferire una regola generale che codifica l’associazione tra gli attributi di un cliente e il suo rischio, ovvero il sistema di Machine Learning adatta un modello ai dati passati per poter calcolare il rischio per una nuova applicazione e quindi decide di accettare o rifiutarlo di conseguenza.
Questo è un esempio di problema di classificazione in cui sono presenti due classi:
- clienti a basso rischio
- clienti ad alto rischio.
Le informazioni su un cliente costituiscono l’input per il classificatore il cui compito è assegnare l’input a una delle due classi.
Dopo l’addestramento con i dati passati (training set), una regola di classificazione appresa può essere della forma:
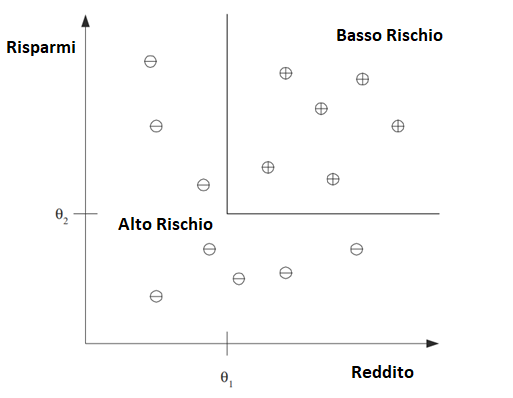
IF (reddito > θ1 AND risparmi > θ2)
THEN
basso rischio
ELSE
alto rischio
per opportuni valori di θ1 e θ2 .
Questo è un esempio di discriminante; è una funzione che separa gli esempi di diverse previsioni. Avendo una regola come questa, l’applicazione principale è la previsione: una volta che abbiamo una regola che si adatta ai dati passati, se il futuro è simile al passato, allora possiamo fare previsioni corrette per nuove istanze.
Data una nuova applicazione con un certo reddito e risparmio, possiamo facilmente decidere se è a basso rischio o ad alto rischio. In alcuni casi, invece di fare un 0/1 (basso rischio/alto rischio), potremmo voler calcolare una probabilità, ovvero P(Y|X), dove X sono gli attributi del cliente e Y è rispettivamente 0 o 1 per il rischio basso o rischio alto.
- P(Y=0/X=x) è la probabilità che il cliente X riesca a pagare
- P(Y=1/X=x) è la probabilità che il cliente X NON riesca a pagare
Da questo punto di vista, possiamo vedere la classificazione come l’Apprendimento di un’Associazione da X a Y. Allora per un dato X = x, se abbiamo P(Y = 1|X = x) = 0.8, diciamo che il cliente ha un 80 percentuale di probabilità di essere ad alto rischio, o equivalentemente una probabilità del 20% di essere a basso rischio. Decidiamo quindi se accettare o rifiutare il prestito a seconda di t lui possibile guadagno e perdita.
Questo è un esempio di discriminante, è una funzione che separa gli esempi di diverse previsioni. Per una regola come questa, l’applicazione principale è la previsione: una volta che abbiamo una regola che si adatta ai dati passati, se il futuro è simile al passato, allora possiamo fare previsioni corrette per nuove istanze.
Segue una figura che mostra l’output di questa classificazione