Supponiamo di voler realizzare un sistema in grado di prevedere il prezzo di un’auto usata con un sistema di apprendimento automatico.
Gli input sono gli attributi dell’auto (marca, anno, cilindrata, chilometraggio e altre informazioni) che riteniamo influenzino il valore di un’auto mentre l’output è il prezzo dell’auto.
Nota: I problemi in cui l’output è un numero sono problemi di regressione.
Siano X gli attributi dell’auto e Y il prezzo dell’auto.
Rilevando le transazioni passate, possiamo raccogliere dati di addestramento e con un programma di Machine Learning e possiamo adattare una funzione a questi dati per apprendere Y in funzione di X.
Un esempio è dato nella seguente figura dove la funzione adattata è della forma:
y = wx + w0 per opportuni valori di w e w0.
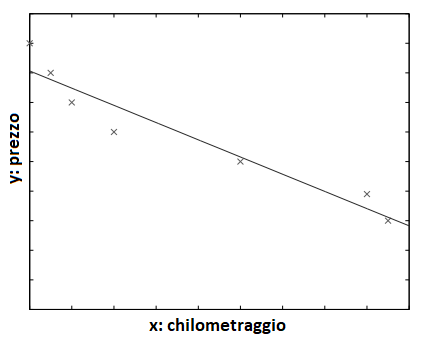
Nota: L’immagine mostra un set di dati di addestramento delle auto usate. Per semplicità, il chilometraggio viene preso come unico attributo di input e viene utilizzato un modello lineare.
Sia la regressione che la classificazione sono problemi di apprendimento supervisionato in cui c’è un input, X, un output Y.
Il compito è imparare la mappatura dall’input all’output. L’approccio nell’apprendimento automatico consiste nell’ assumere un modello definito e un insieme di parametri:
y = g(x|θ)
dove g(·) è il modello e θ sono i suoi parametri.
Ma tra Classificazione e Regressione vi sono due differenze importanti relative all’output y e al modello g(·):
- In un problema di classificazione y è un codice di classe mentre in un problema di regressione è un valore numerico.
- In un problema di classificazione g(·) è la funzione discriminante che separa le istanze di classi diverse mentre in un problema di regressione è la funzione di regressione.
Il programma di machine learning ottimizza i parametri, in modo tale che l’errore di approssimazione sia ridotto al minimo, ovvero le nostre stime siano il più vicino possibile ai valori corretti forniti nell’addestramento. Ad esempio, nella figura 1.2, il modello è lineare e w e w0 sono i parametri ottimizzati per il miglior adattamento al training set.
Nei casi in cui il modello lineare è troppo restrittivo, si può usare ad esempio un modello quadratico o un polinomio di ordine superiore, o qualsiasi altra funzione non lineare dell’input, questa volta ottimizzando i suoi parametri per il miglior adattamento.
